미·적분 등 개념 확실히 이해해야 응용문제 대비할 수 있어

[논술 A to Z] 2014학년 이화여대 논술 기출문제 분석

날씨가 점점 추워지고 있다. 이 말은 대학수학능력시험(수능)이 코앞에 다가왔다는 뜻으로, 60만 수험생에게는 정말 중요하고 또한 힘든 마지막 시즌이 찾아온 것이다. 정시에 올인하는 학생들은 수능이 끝나면 어느 정도 긴장의 끈을 놓아도 되겠지만, 수시에도 지원을 하는 대다수의 학생들에게는 수능 끝난 이후 한 주가 더욱 중요하다고 할 수 있다. 많은 수시 논술고사가 수능이 끝난 주, 혹은 그 다음주에 실시되기 때문이다. 수능을 치르고 바로 논술고사를 봐야 하기 때문에 논술 준비를 충분히 하지 못한 채 논술고사를 치르는 수험생이 많다.

주어진 시간이 부족할 때, 우선순위는 최근 기출문제, 모의논술, 유사문제, 예상문제 순이며, 중점적으로 공부를 해야 하는 단원 역시 가장 많이 출제되는 미적분, 수열과 극한, 공간도형과 벡터 순이 될 것이다. 또 수리 논술 문제는 개념들의 의미를 깊게 물어보는 문제들이 많기 때문에 반드시 스스로 개념에 대한 의미를 꼭 짚어보고 확실히 이해를 해놓아야 응용문제에도 대비할 수 있다.

2014학년도 이화여대 수리논술은 어려워 많은 학생이 접근하지 못했다. 그러나 정적분의 기본 개념과 의미를 알고 조금만 생각하면 충분히 풀 수 있다. 사진은 지난해 이화여대에서 수험생들이 수시모집 논술고사를 치르는 모습.
세계일보 자료사진

적분의 대표적인 유형인 정적분의 의미를 묻는 2014학년도 이화여대 기출문제를 한 번 같이 보자.

이 문제는 어려워 대다수는 접근을 잘 하지 못했다. 앞서 미분 문제가 나왔는데, 미분은 학생들이 비교적 쉽게 접근할 수 있었다. 그것은 학생들에게 익숙한 ‘미분가능’, ‘도함수’, ‘연속’에 대한 질문들이었기에 처음에 문제를 접할 때 큰 부담이 없었다.

반면에 적분 문제는 이계도함수와 알 수 없는 적분이 들어간 부등식이 나오니 학생들 마음속에서는 이미 ‘내가 못 푸는 어려운 문제가 나왔구나’ 하며 처음부터 겁을 먹은 것이다. 그러나 정적분의 기본적인 개념과 그 의미를 알고 있는 학생이라면 조금만 생각을 하면 충분히 풀 수 있는 문제라는 것을 알 수 있을 것이다.

문제를 풀기에 앞서 제시문에 나와 있는 정보들을 찾아보자. 지난 기사(세계일보 2014년 7월21일자 참고)에서 언급했듯이 제시문과 논제에 답이 있다고 했다. 제시문을 살펴보면 함수 f(x)가 연속이고, 미분가능하며, 증가한다고 하였는데, 여기에서 우리는 이 글로 쓰인 문장을 쉽게 이해할 수 있는 간단한 수식, 즉 수학적 표현으로 바꿔주어야 한다(세계일보 2014년 7월27일자 참고).

미분가능한 함수 f(x)가 증가한다는 것은 f(x)의 도함수인 f’(x)가 0 이상이라는 의미이다.

따라서 제시문에 주어진 조건은 f’(x)≥0으로 바꿔줄 수 있다. 또한, g(x)가 f(x)를 적분한 함수이므로 의 양변을 미분하면, g’(x)=f(x)라는 수식을 얻을 수 있다. 이 두 가지 정보를 제시문에서 얻은 후, 1번 문제를 풀어보자.

1번 문제에서 g(x)의 이계도함수인 g’’(x)에 대해 물어보았으므로 우리는 당연히 g’(x)를 미분하여 구하면 된다. 여기에서 바로 앞에서 제시문에서 얻은 정보인 g’(x)=f(x), f’(x)≥0을 이용하면, 너무나 쉽게 풀 수가 있게 된다.

(풀이)

f(x)는 증가함수이므로 f’(x)≥0,

의 양변을 미분하면, g’(x)=f(x)이 식의 양변을 한 번 더 미분하면 g’’(x)=f’(x)가 되고, f’(x)≥0이므로 g’’(x)≥0가 성립한다.

2번 문제로 넘어가기에 앞서 수리논술의 가장 큰 특징 하나를 짚고 넘어가자. 수리논술은 하나의 큰 문제에 3∼5개의 작은 문제들이 달려 있는 형식을 갖추고 있다. 

여기에서 1번 소문제는 비교적 난이도가 낮은 편이고 뒤쪽으로 갈수록 점점 난도가 높아진다. 수리논술은 단순히 수학을 잘 하는 학생을 뽑기 위한 문제를 출제하는 것이 아니라 논리적 사고가 가능한 학생들을 뽑기 위한 문제를 낸다.

다시 말해 비교적 쉬운 1번 문제를 풀면, ‘반드시’ 앞의 문제들을 이용해 다음 문제를 풀 수 있도록 출제한다는 이야기이다. 그렇다면, 우리는 1번 문제를 잘 푼 데에 그치지 않고 1번의 결과가 어떤 의미를 가지는지 한 번 더 생각을 할 필요가 있다는 뜻이다.

g’’(x)≥0가 의미하는 것은 g(x)가 ‘아래로 볼록’이라는 것이다. 너무나 당연한 우리가 모두 알고 있는 얘기지만, 이 의미를 한 번 짚고 넘어가는 학생과 그냥 g’’(x)≥0만 구하고 넘어가는 학생 간의 차이는 그 다음 문제를 접근할 때 큰 차이를 보여준다.

자, 그럼 2, 3번 문제를 한번에 해결해보자. 정적분 문제는 그래프에서 함수를 그렸을 때 적분값이 의미하는 바를 알 수 있다면 비교적 간단하게 풀 수 있다.

g(x)는 정의에 의해 g(0)=0을 만족하고, 증가함수인 f(x)를 0부터 x까지 적분한 값이기 때문에 증가한다는 것을 알 수 있다. 따라서 아래로 볼록인 증가함수 g(x)를 쉽게 그릴 수 있다.

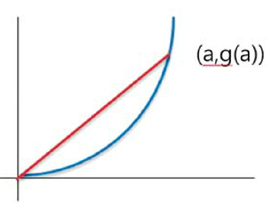
구간 [0,a]에서 식이 나와 있으므로 그 구간에 대해서만 생각해보자. 문제 2의 우변인 가 의미하는 게 어떤 것인지 그래프에서 보면, 기울기가 g(a)/a인 원점을 지나는 직선 식이 된다. 그리고 이 직선식은 (a,g(a))를 지난다는 것을 알 수 있다.

그래프로 그리면 아래 그림과 같이 나타낼 수 있고, 함수 g(x)는 아래로 볼록이기 때문에 직선식 g(a)/a x보다 항상 작거나 같다는 것을 알 수 있다. 

문제 3의 우변은 g(x)를 0부터 a까지 적분한 값이므로 x축과 y=g(x), x=a로 둘러쌓인 부분의 넓이(파란색 빗금)이다. 좌변이 의미하는 바가 무엇인지를 한 번 생각해보자.

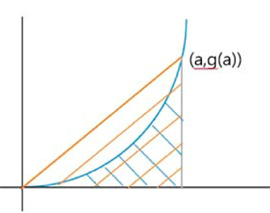
이므로 좌변은 ag(a)/2가 되는데 이는 그래프에서 x축, y축, x=a, y=g(a)로 둘러쌓인 직사각형 넓이의 절반, 즉 원점과 (a,g(a)), (a,0)을 꼭지점으로 하는 삼각형의 넓이(주황색 빗금)라는 것을 알 수 있다. 문제 2에서와 마찬가지로 g(x)는 아래로 볼록이기 때문에 삼각형 넓이가 더 큰 값을 가지게 된다. 

조홍재 아토즈 논술 수리논술 강사

위와 같이 간단한 그래프를 통해 적분에 대한 문제를 쉽게 해결해 보았다. 수리 논술 문제는 고교 과정을 충실히 공부한 학생이라면 충분히 풀 수 있는 문제라고 하지만, 정작 학생들이 시험장에 들어가 문제를 받으면 한 문제도 제대로 시작도 못하는 경우가 태반이다.

이는 수능이나 내신 공부를 하면서 문제를 푸는 방법이나 유형만 익혔을 뿐, 원리에 대한 이해가 잘 안 된 학생들이 많기 때문이다. 이런 이해를 하기 위해서는 평소부터 수학 문제를 풀거나 개념을 익힐 때 머릿속으로 확실히 이해하고 넘어가는 과정을 습관화시키는 것이 필요하다.

지금 당장이라도 교과서나 아무 참고서를 펼쳐서 미분과 적분 부분을 한번 찾아 읽어보자. 문제를 풀지 말고 중요한 개념들을 읽고, 머릿속에서 어떤 의미를 지녔는지 한번 생각해보자.

미분과 적분의 정의가 무엇인지 그리고 그래프에서 이것들이 의미하는 바가 무엇인지. 적은 시간을 투자하더라도 생각을 하는 습관을 들인 사람과 그렇지 않은 사람과는 나중에 시험장에서는 큰 차이가 날 것이다.

조홍재 아토즈 논술 수리논술 강사