[영상] 손가락 열 개로 셀 수 있는 최대 숫자는?

어릴 적 처음 숫자를 배웠을 때부터 지금까지 우린 열 손가락을 하나씩 접어가며 수를 세어왔다. 인류가 10을 기수로 한 십진법을 일반적으로 쓰는 건 손가락이 10개이기 때문이다. 참고로 십진법은 한 자리씩 올라갈 때마다 자릿값이 10씩 커지는 올라가는 수 체계다.

양손으로 10보다 더 큰 숫자를 한 번에 셀 수는 없을까? 해외 매체 인디100이 수학자 제임스 탠튼의 숫자 세기 방법을 소개했다. 그가 TED-Ed 영상에서 공개한 바에 따르면 열 손가락만으로 무려 59048까지 셀 수 있다. 



10
10은 쉽다. 손가락 하나당 1씩 더하면 된다.



24
손가락 한 개를 3개 부분으로 나눠보자. 각 부분을 짚을 역할을 하는 엄지를 제외한 나머지 손가락은 전부 네 개다. 따라서 한 손당 총 12까지 셀 수 있다. 양 손이면 12 x 2 = 24다.

60
만약 오른손을 전부 접어 12를 셌을 때마다 왼손 손가락을 1개씩 접는다면 어떨까? 이 경우 양손으로 셀 수 있는 숫자는 12 x 5 = 60까지 늘어난다.   

144
조금 더 응용해보자. 왼손도 앞선 방법에 따라 12까지 셀 수 있다. 따라서 오른손 전체로 12롤 한 번 셌을 때마다 왼손으로 숫자를 센다면 12 x 12인 144까지 셀 수 있다.



576
이번엔 좀 다른 방법이다. 손가락이 접히는 부분의 선까지 지표로 삼는 것이다. 한 손가락 당 6부분이므로 엄지를 제외한 네 손가락은 총 24부분으로 나뉜다. 이전과 마찬가지로 엄지는 각 부분을 짚는 역할이다. 따라서 한 손으로 24까지 셀 수 있으므로 양손이면 24 x 24 = 576이 된다.


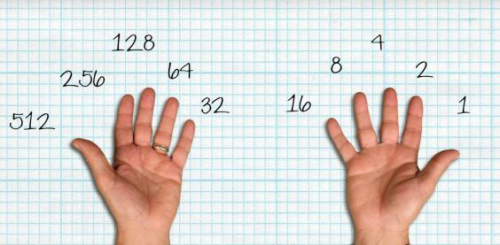
1023
이 부분부턴 수학적인 계산이 필요하다. 모든 자연수는 이진법으로 표현 가능하므로 이진법을 이용하면 더 큰 수까지 셀 수 있다.

각 손가락에 2의 0제곱, 2의 1제곱, 2의 2제곱... 2의 9제곱을 대응시킨다. 즉, 순서대로 1, 2, 4, 8, 16, 32, 64, 128, 256, 512다.

7은 1+2+4이므로 이를 표현하려면 순서대로 첫째, 둘째, 셋째 손가락을 접는다. 다만, 숫자 하나가 어떠한 2의 제곱 조합으로 구성되는지 생각해내는 일은 쉽지 않을 듯싶다.

59048
손가락 한 개로 3가지 상태를 나타낼 수 있다면 더 큰 수도 가능하다. ‘완전히 펴기‘, ‘반만 접기‘, ‘완전히 접기‘가 그것이다.

열 손가락에 차례로 3의 0제곱, 3의 1제곱, 3의 2제곱... 3의 9제곱까지 대응시킨다. 그 후 3가지 상태에 따라 0, 1, 2를 순서대로 곱한 수를 표현한다.

즉, 3의 0제곱(=1)인 오른손 엄지를 완전히 펴면 1 x 0 = 0, 반만 접으면 1 x 1 = 1, 다 접으면 1 x 2 = 2가 되는 것이다. 이 경우 각 손가락이 표현할 수 있는 가장 높은 숫자는 첫 번째 손가락 2(2x3의 0제곱)부터 6, 18, 54, 162, 486, 1458, 4374, 13122에 이어 열 번째 손가락에서는 39366(2x3의 9제곱)이 된다. 이를 다 더하면 59048인 된다.

따라서 이러한 계산에 따르면 59048까지 세는 게 가능하다.

해당 방법을 소개한 수학자 제임스 탠튼은 지적 능력과 손가락의 유연함에 따라 더 큰 숫자도 셀 수 있다고 조언한다. 하지만 현실적으로 1024 이후부터 이 방법을 얼마나 많은 사람이 활용할지는 의문이다.




나진희 기자 [e-mail]